E' solo il mio punto di vista...e, come mi è stato fatto notare da alcuni lettori che ringrazio, premetto che non è intento di questa pagina confutare l'importanza di una adeguata composizione grafica secondo regole auree o altre note che ne evidenziano punti di forza e di interesse, ma quella di evidenziare il comportamento sempre più frequente di fotografi che leggono un qualche articolo fotografico e scaricano l'immagine della spirale aurea.
Ormai sembra non avere più un significato numerico, ma molti la usano come stereotipo da sovrapporre ad una foto, cercando un qualsiasi elemento della foto che si sovrapponga ad un punto della spirale (confusa con l'ente SEZIONE AUREA) e poi dire che quella foto è perfetta. Spesso il punto di interesse scelto è un qualsiasi elemento della foto preso a caso... "Il sassolino 129 in basso a sinistra" di quel masso di ghiaia".
Mi è capitato di leggere frasi allegate a foto di paesaggio del tipo:
" Uhm... peccato che il fiore non sia capitato nel centro della spirale, altrimenti la mia foto sarebbe stata perfetta", oppure:
" Guardate l'uccello, il sasso e quella nuvola... si trovano sulla linea della spirale; ho realizzato una foto perfetta";
ma peggio ancora mi è anche capitato di vedere spirali deformate, fuori proporzione aurea, adattate alle foto cercando di farle passare su elementi della foto voluti (ritagliando anche grandi porzioni della foto e tutto quello che non ci va dentro), nella speranza di ottenere una foto perfettamente composta. Spesso addirittura sulla spirale non vi sono neanche elementi o linee costruttive tangenti, ma è li solo per sovrapposizione.
Non mi viene quasi mai da ridere perchè in questo modo capisco che non è chiaro il concetto matematico di Sezione Aurea e soprattutto che non è chiaro il valore che essa ha acquisito nel tempo nei vari campi artistici.
E' un pò come il concetto di MODA, ente matematico statistico che analizza la storia, il passato: mi viene da riflettere quando sento dire "L'inverno prossimo andrà di moda il nero!!!", parlando del futuro.
Ora, pur non avendo chiaro il concetto matematico di "MODA" e accettando quanto afferma tale frase, non è che se compro una camicia nera e me la butto addosso, posso definirmi il BRAD PITT dell'inverno!!
Chiarito questo doveroso punto veniamo a definire l'ente "phi" (o Sezione Aurea) che rappresenta il valore numerico di una proporzione.
La Sezione Media ed Estrema, poi divenuta Auerea: questa sconosciuta
Dato un segmento (AC), somma di due segmenti (AB)+(BC), si ottiene una sezione aurea quando il segmento più corto (BC) sta al segmento più lungo (AB) come il segmento più lungo (AB) sta al segmento intero (AC).
La proporzione sarà così espressa: BC: AB=AB: AC .
Risolvendo l'equazione, con semplici passaggi matematici, otterremo come proporzione dei segmenti (AB) e (BC) il valore "phi", un numero irrazionale detto anche "numero d'oro":
0,618034... / 0,381966... = 1,61803398874989...
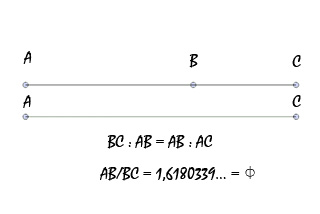 |
Proporzione Media ed Estrema di due segmenti |
Tale valore è, allo stesso tempo, il valore limite del rapporto tra due elementi consecutivi della successione ricorsiva di Fibonacci, per un numero n che tende all'infinito (che risulta una buona approssimazione del valore irrazionale "phi"). La successione di Fibonacci è rappresentata dai numeri:
0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584...
e al crescere di n, il valore prima identificato approssima sempre più il valore "phi".
8/5=1,6; 21/13=1,615; 233/144=1,61805; 2584/1597=1,618033813...
Partendo da questo valore "phi" potremo definire il segmento e anche le altre forme auree, quali il rettangolo, il triangolo, il pentagono, la spirale...
Chiaramente tali enti geometrici avranno come elemento base di costruzione "phi", superfluo dirlo, quindi saranno rettangoli, spirali ecc... con definiti metodi costruttivi e definite proporzioni intrinseche.
Vediamo ad esempio la costruzione di un rettangolo aureo:
Consideriamo un quadrato di lato AB=1; da questo è possibile costruire un rettangolo aureo semplicemente individuando il punto medio di un lato e da qui disegnare la circonferenza passante per il vertice opposto.
L'intersezione della circonferenza con il prolungamento del lato sul quale essa è centrata ci darà il punto estremo C che individuerà il segmento AC, secondo lato del rettangolo aureo. Con un pò di matematica (partendo dal teorema di Pitagora) avremo:
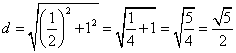 |
Diagonale del rettangolo |
Questa lunghezza è quella che si andrà a sommare all'altrà metà del segmento AB utilizzato ottenendo cosi la lunghezza del segmento AC:
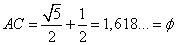 |
Lunghezza del lato AC |
Provando a disegnarlo:
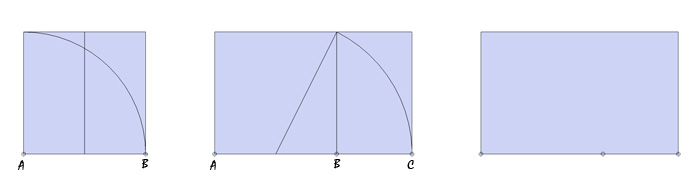 |
Costruzione geometrica del rettangolo aureo |
E' proprio la costruzione di tali enti geometrici che accosta "phi" alle arti o meglio alle rappresentazioni artistiche, anche se alle volte è fatto in maniera molto forzata ed impropria (come negli esempi di apertura).
Possiamo ritrovare la proporzione aurea anche in storiche costruzioni quali il partenone e Notre Dame, nelle opere artistiche di Leonardo da Vinci e Botticelli.
Fu nell'800 che la "proporzione divina" venne definita "sezione aurea" e andò sempre piu diffondendosi anche nel campo dell'arte.
Furono gli artisti stessi ad ammettere l'utilizzo di questa particolare proporzione nella progettazione e poi costruzione con la convinzione che il "rettangolo aureo" fosse la chiave dell'armonia delle loro opere, influenzati anche dai numerosi studi che ne avevano certificato la presenza in natura.
L'odierno abuso in fotografia: pratica di molti fotografi
Tuttavia il legame tra tale valore "phi" e l'armonia di una composizione è solo dovuto ad risultato statistico, dato dall'analisi di un vasto ma comunque limitato numero di campioni. In pratica si è riscontrato un maggior gradimento da parte di un numero di campioni di osservatori, di opere che hanno intrinseco nella loro realizzazione questo rapporto divino, grazie a studi in campo psicologico di Gustav Fechner, volti a far emergere la testimonianza di una tendenza inconscia verso la proporzione aurea.
Non metto in dubbio che ci siano opere dove è stato ritrovato questo rapporto che, per coincidenza o no, riscontrino il mio gradimento e probabilmente quello di molti altri o che in molte strutture della natura sia stato riscontrato tale valore costruttivo; si ha spesso evidenza della gradevole composizione che risulta avere un'opera costruita secondo alcune regole costruttive che hanno come elemento la sezione aurea.
Quello che invece non riesco a comprendere è l'utilizzo che ne fanno alcuni fotografi che usano l'immagine di una spirale aurea sovrapposta ad una loro foto per decantarne la perfezione.
Secondo me sovrapporre una spirale aurea o un pentagono aureo ad una foto scattata e scoprire che la foto presenta alcuni punti chiave sovrapposti a punti di convergenza della rappresentazione aurea non vuole assolutamente dire che quella foto sia perfetta in nome di qualcosa; al massimo potrà avere un gradimento da parte di una percentuale di popolazione (difficilmente quantificabile);
Ciò che sarebbe importante è avere questi gradimenti, non influenzando la popolazione con la sovrapposizione della rappresentazione aurea, poiche spesso sarà questa deviazione mediatica e quell'alone di misticismo a far piacere quella data foto.
Peggio ancora se poi si è costretti a riadattare forzatamente una spirale per farla combaciare.
Quindi diciamocelo con franchezza una composizione secondo una sezione aurea sarà gradevole a prescindere che vi sia impressa o meno sopra una spirale e sarà bellissimo scoprirlo e mostrarlo ad altri osservatori.
Se la foto invece non è gradevole, non concepita bene alla nascita, non c'è rappresentazione aurea che tenga, potremo trovare mille rapporti aurei all'interno tramite ritagli vari, tramite riduzione, ma l'opera rimarrà sempre meno gradevole.
Questo farebbe riflettere chiunque che tali proprietà di armonia, date dall'adottare tale ente nella composizione fotografica, si acquisiscono a priori, curandone realmente la composizione allo scatto, (quindi decidendo prima se questo avrà una composizione seguendo una regola aurea) e non cercare di sovrapporre forzatamente una spirale, triangolo ecc... cercando di orientarli in chissà quali versi, con realativi vizi di forma... per poi dire:
" Cavolo se quell'elemento fosse stato qui, la mia foto sarebbe stata perfetta".
Il Michelangelo e tutti gli altri sapevano a priori come e cosa stavano realizzando...
La regola dei terzi
Nella fotografia ora è norma comune affidarsi ad una semplificazione o meglio approssimazione della proporzione aurea. Non avendo uno standard ben definito dei sensori e delle dimensioni di essi, si approssima un rettangolo aureo con un rettangolo che ha i lati suddivisi in terzi, che risulta molto più facile da rappresentare negli specchi e nei mirini ottici delle macchine fotografiche per aiutare la composizione. La cosidetta regola dei terzi che prevede l'utilizzo dei punti di intersezione dei terzi come punti focali di interesse. Per cercare di mantenere una composizione quanto più vicina alla composizione aurea sarebbe preferibile considerare la zona più interna del rettangolo rispetto ai terzi cosi da avvicinarsi di più alle linee di costruzione auree.
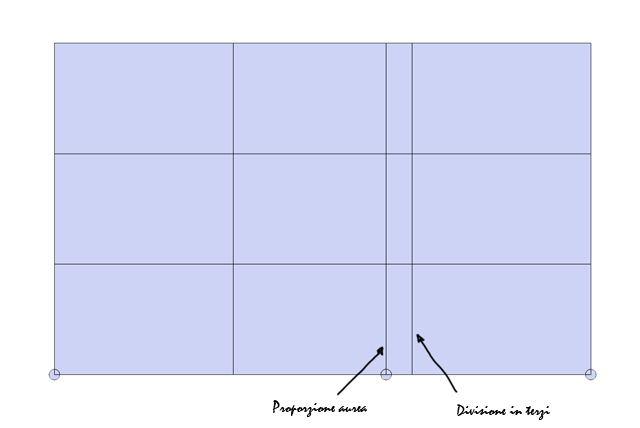 |
Sovrapposizione sezione aurea e regola dei terzi |
In definitiva spesso mi chiedo come provocazione, data la grande rilevanza che avrebbe una composizione in un rettangolo aureo (dico una composizione non studiata a priori):
"Perchè il rettangolo più usato al mondo non adotta queste proporzioni... Cavolo quanti fogli A4 si consumano da moltissimi anni in moltissimi campi. Perchè non adottare questa proporzione, qualsiasi lettura acquisirebbe già maggior interesse da parte del lettore"...
oppure: "Perchè un sensore (o già da allora, una pellicola) non è stata progettata con proporzioni auree?? Non avrebbe già dato una marcia in più ad una foto ancora prima che questa fosse scattata?"
Magari avremmo detto:" Qualsiasi immagine verrà impressa qui sopra sarà perfetta".
Evidentemente non basta solo far cascare un'immagine dentro un rettangolo o dentro una spirale.
Siate liberi di comporre secondo il vostro gusto e gradimento e accettate il fatto che possa essere condiviso o meno dagli altri osservatori.

